Robust Collaborative SLAM
This research project deals with the question of how to robustly (with respect to sensor errors or even sensor failures) localize an autonomous vehicle and simultaneously create a map of its environment (SLAM). Optimization based SLAM approaches often suffer the convergence problem [1], meaning that an optimization algorithm does not always find a global minimum if many local minima are present. Furthermore, filter based SLAM approaches often suffer the inconsistency problem (i.e. the estimates are overconfident and the result is actually less precise than indicated) since the different sources of error (e.g. sensor and extrinsic transformation errors) might not follow a Gaussian distribution and even exhibit nonzero mean errors (i.e. biases). Moreover, even if the errors are zero-mean Gaussian, the result can be inconsistent if the linearization point is far from the true solution [1]. However, autonomous vehicles are safety-critical systems for which it is important to know the actual pose uncertainty in order to take this uncertainty into account for further operation. To increase the robustness with respect to sensor errors or even sensor failures, information from multiple sensors must be fused. However, the errors of different sensors and the inter-sensor errors (e.g. the uncertain extrinsic transformation between sensor coordinate systems) exhibit different error characteristics. For example, some sensor errors may follow a Gaussian distribution, some errors may follow a normal distribution, and some error distributions may be unknown. With conventional SLAM methods such as an Extended Kalman Filter or an optimization based approach, it is difficult to consistently take these errors into account and propagate them to the results.
Thus, I previously proposed an interval-based approach to compute the motion of a robot (i.e. dead reckoning) between discrete points in time using information from a camera, LiDAR and the gyroscope of an IMU [2]. In this project, the previous approach shall be extended by formulating the SLAM problem as a continuous-time Constraint Satisfaction Problem (CSP) that can be solved using interval analysis tools. To move from a discrete-time computation of the robot pose to a continuous-time formulation, derivative information such as the velocity, acceleration or angular rates are required. Thus, information from additional sensors such as wheel odometers or the accelerometer of an IMU must be integrated into the existing approach. Consequently, in addition to the bounded error models introduced for camera, LiDAR and gyroscope [3, 4], new bounded error models for odometers and accelerometers are required.
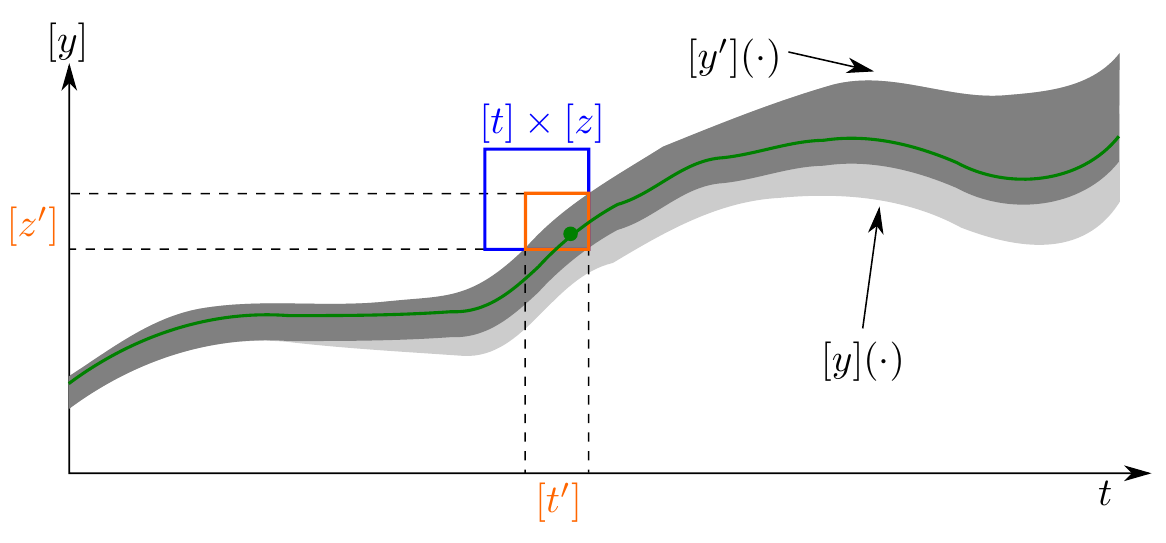
Due to the integration of derivative information, the pose of the robot is no longer only known at discrete points in time and space, but is continuously defined as a set of trajectories, also known as tubes [5]. This allows to propagate local information (e.g. a discrete GNSS measurement or an observation of a known landmark) over the whole tube domain to refine the previous pose estimates and consequently also refine the built map. The following figure shows an example:

Local information cannot only be obtained using the robot’s own sensors, but also using observations of other vehicles. Consequently, the approach can be extended to Collaborative Positioning by extending the CSP by constraints introduced by other nodes in the dynamic sensor network (e.g. a drone observes the car and computes its pose). However, this poses additional challenges, since the information cannot be assumed to be perfectly synchronized, and therefore the information is uncertain not only with regard to the pose estimate, but also with regard to when this pose estimate was acquired. For stochastic approaches, it is difficult to propagate this kind of time uncertainty through the nonlinear equations. In contrast, as Figure 2 shows, using tubes this time uncertainty can be taken into account in a straightforward way [6]. The main advantage is that observations from complementary sensors can be easily combined, since only bounds on the observations and bounds on the timestamps of the observations are required. In particular, this enables data from sensors with different measuring rates to be fused, which can even be asynchronous.
Nevertheless, this raises the question of how to assess this time uncertainty, i.e. the synchronization error between multiple nodes in a dynamic sensor network. Here, I plan to extend my preliminary work on the synchronization of sensors in a laboratory [3, 4]. Depending on the connectivity of the sensors, it is conceivable to provide a generic solution that is not based on sensor data, but uses a network approach similar to the Network Time Protocol (NTP).
In addition, an open question of interval-based SLAM is which features should (or can) be reliably detected with which sensors to subsequently insert them into the map. Subsequently, this also raises the question of how a guaranteed association of features extracted from sensor data and features in the map can be performed. Similarly, a guaranteed association must also be performed for measurements of known landmarks. Afterwards, these associations allow to reduce the uncertainty of the robot’s pose and can thus be employed as local information to contract the tube.
Another important aspect of the SLAM problem is the detection of loop closures. Under the assumption of unknown but bounded errors, Rohou et al. show that it is possible to prove that a loop has been closed using only information from proprioceptive sensors (e.g. an IMU) [7]. This kind of proof cannot be achieved using stochastic methods. Consequently, this project aims to extend this guaranteed detection of loops to also incorporate information from exteroceptive sensors. Again, this requires a method to generate guaranteed associations between sensor and map data. Since some of the proposed concepts have been successfully applied for underwater robots, a major part of this research project is to transfer these concepts and validate their applicability to autonomous vehicles. Thus, real experiments with a dedicated platform are required. Ideally, a car should be permanently equipped with sensors for these experiments. The classification into the research training group i.c.sens is apparent. First, the concept of integrity is considered by using interval analysis to consistently model errors. To further improve the integrity of the system, information from multiple sensors shall be fused. Second, the formulation of the SLAM problem as a continuous-time CSP also allows the collaboration aspect of i.c.sens to be taken into account. As explained, local information from multiple vehicles can be fused to improve the pose estimates and the built map.
[1] S. Huang and G. Dissanayake, “A critique of current developments in simultaneous localization and mapping”, International Journal of Advanced Robotic Systems, vol. 13, no. 5, pp. 1-13, Sep. 2016.
[2] R. Voges and B. Wagner, “RGB-Laser Odometry Under Interval Uncertainty for Guaranteed Localization”, in Book of Abstracts of the 11th Summer Workshop on Interval Methods (SWIM 2018), Jul. 2018.
[3] R. Voges and B. Wagner, “Timestamp Offset Calibration for an IMU-Camera System Under Interval Uncertainty”, in IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, Oct. 2018.
[4] R. Voges and B. Wagner, “Extrinsic Calibration Between a 3D Laser Scanner and a Camera Under Interval Uncertainty”, in Book of Abstracts of the 12th Summer Workshop on Interval Methods (SWIM 2019), Palaiseau, France, Jul. 2019.
[5] S. Rohou, L. Jaulin, L. Mihaylova, F. Le Bars, and S. M. Veres, “Reliable Robot Localization: A Constraint-Programming Approach Over Dynamical Systems”, ISTE LTD, Jan. 2, 2020, 284 pp.
[6] S. Rohou, L. Jaulin, L. Mihaylova, F. L. Bars, and S. M. Veres, “Reliable non-linear state estimation involving time uncertainties”, Automatica, vol. 93, pp. 379-388, Jul. 2018.
[7] S. Rohou, P. Franek, C. Aubry, and L. Jaulin, “Proving the existence of loops in robot trajectories”, The International Journal of Robotics Research, vol. 37, no. 12, pp. 1500-1516, Oct. 2018.